Perhaps the easiest way to solve an equation with rational expressions (i.e., fractions) is to multiply both sides of the equation by the least common multiple of all the denominators. Multiplying through will eliminate all the denominators, so there will be no fractions remaining. From there, the equation will usually be either quadratic or linear and should be relatively straightforward to solve. Remember to check that none of your solutions make any denominator in the original equation equal zero.
When a variable is under a radical, both sides of the equation will need to be squared. Before doing this, isolate the radical term. (When there are two radical terms, it is typically easier to separate them before squaring both sides for the first time.) After squaring both sides of the equation, you will usually be left with a quadratic or linear equation to solve. Remember to check for extraneous solutions! When you square both sides of an equation, you open the door to extraneous solutions, so you have to check them by plugging them into the original equation.
P.5 dealt primarily with absolute value and inequalities.
Definition of absolute value:
|x| = a if and only if x = a or - x = a
for inequalitites:
|x| < a if and only if x < a or - x < a
Example:

Using interval notation, we would represent our solution as [2,3].
Polynomial inequalities are a big part of P.5. Solving them is more complicated than solving equations.
Before the official solving begins, you must have a zero on one side of the inequality.
The first to solve a polynomial inequality is to find the zeros of the polynomial.
Use these zero to set up intervals, and then pick a test value in each interval.
Plug each test value into the polynomial and see if its value is positive or negative.
Your solution will include all the intervals that matched your inequality (+ for >0 and - for <0).
This process makes more sense when you consider the graph of your inequality. The inequality is >0 when its graph is above the x-axis and <0 when its graph is below the x-axis. Setting up the test intervals is a numeric way of making that determination.
Example:
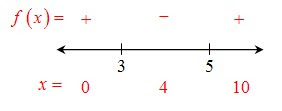
The first order of business is to find the zeros of the polynomial.
Next, plot the zeros on a number line to establish the test intervals, then choose a test value from each interval. Plug that value into the polynomial and determine if the polynomial's value is postive or negative.
We were interested in where the polynomial was <0, so we choose the interval where f (x) was negative.
Using interval notation, we would express our solution as (3,5).
Below is the graph of the polynomial. Looking at that, it is clear that the interval where the graph is below the x-axis (<0) is from 3 to 5.



No comments:
Post a Comment