The inverse of a function is when all of the x and y coordinates are switched.
Example: The inverse of (1,2) (2,4) (3,6) is (2,1) (4,2) (6,3)
To find the inverse of a function you must switch the x and y variable and then solve for y. This is denoted by  . The domain of
. The domain of 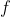 must be equal to the range of
must be equal to the range of  , and the range of
, and the range of 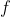 must be equal to the domain of
must be equal to the domain of  .
.
Example: If 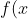=x+4) then
then 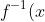=x-4)
To verify that you found the inverse of the function you can compose one to the other and it should equal x. If it doesn't then you did something wrong.
Example: 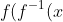)=f(x-4)=(x-4)+4=x)
The graph of a function and its inverse are reflected across the line 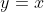 .
.
Example: The red graph is 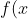=3x+3) and the green graph is
and the green graph is 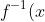=(x-3)/3) .
.

Not all functions have inverses that are functions.
Example:
The red graph is 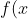=x^2)
The green graph is the inverse which is 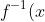=\pm%20\sqrt{x})
The inverse if the red graph (green graph) is not a function because it doesn't pass the vertical line test.

Who ever wrote this is really smart.
ReplyDelete