PreCalculus A (3rd Hour, Fall 2011): 2.4: Complex Numbers

The Complex Number System:

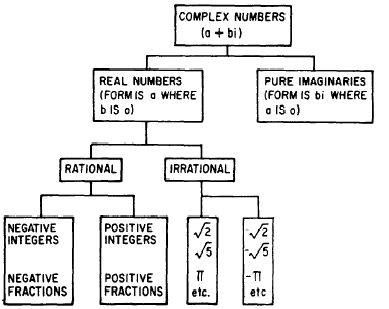
i is an imaginary number

i = √-1, so i² = -1

standard form of a complex number: a + bi

Operations with Complex Numbers:

Addition: add like terms

(3 + 7i) + (9 + 6i)

3 + 9 + 7i + 6i

12 + 13i

Subtraction: subtract like terms

(4 + 5i) - (2-3i)

4-2 + 5i-(-3i)

2 + 8i

Multiplication: distribute

(3 + 2i)(1 + 2i)

3 + 6i + 2i + 2i²

3 + 8i + 2(-1)

1 + 8i

Division: multiply by the complex conjugate

$\frac{2+4i}{6+5i}$

$\frac{2+4i}{6+5i}\cdot \frac{6-5i}{6-5i}$

$\frac{(2+4i)(6-5i)}{36+25}$

$\frac{12-14i-20i^{2}}{61}$

$\frac{32-14i}{61}$

$\frac{32}{61} - \frac{14}{61}i$

Finding i to any power:

$i^{1} = i$

$i^{2} = -1$

$i^{3} = -i$

$i^{4} = 1$

$i^{5} = i$

$i^{6} = -1$

$i^{7} = -i$

$i^{8} = i$

this pattern repeats itself forever and ever

So if you wanted to find i to a really high power, like:

$i^{327}$

you would need to divide the exponent, 327, by 4 to find what number in the pattern it stops at.

327/4 = 81 with a remainder of 3 (which is really the only part that matters to us)

Since the remainder is 3, the answer will be the same as i to the power of 3, which is -i

so:

$i^{327}= -i$

PreCalculus A (3rd Hour, Fall 2011)