Section 4.7

Inverse Trigonometric Functions

As learned in previous chapters, functions can only have inverses if they are one to one, if each of their x values have only one y value and each y value has only one x value. Obviously, sine, cosine and tangent functions are not one to one, as their graphs all fail the horizontal line test miserably.

SINE

COSINE

TANGENT

But these functions do have inverses.

How? By setting a very small domain for each function that allows each function to become one to one.

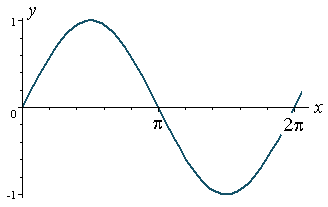
As you can see from the picture below, in this small chunk of the graph, this sine function is one to one.

This is because its domain is [-π/2, π/2].

To have an inverse:

Sine:

Domain:[-π/2, π/2]

Range: [-1, 1]

Because the inverse flips the domain and range:

-Sine:

Domain: [-1, 1]

Range: [-π/2, π/2]

The cosine function has a different domain than the sine function

To have an inverse:

Cosine:

Domain: [0, π]

Range: [-1,1]

And again:

-Cosine:

Domain; [-1, 1]

Range: [0, π]

The tangent function is easier than the sine and cosine functions, as it is just one period of the graph.

To have an inverse:

Tangent:

Domain: [-π/2, π/2]

Range: [-∞, ∞]

Other Things to Remember:

-The output of an inverse trig function is ALWAYS an angle.

All Inverse functions posses the properties:

f[ƒ⁻¹(x)] = x and ƒ⁻¹[f(x)] = x

These properties are also used with inverse trig functions

If -1 ≤ x ≤ 1 and (π/2)≤ y ≤ π, then

sin(-sin x) =x and –sin(sin y) =y

If -1 ≤ x ≤1 and 0 ≤ y ≤ π, then

cos(-cos x) = x and –cos(cos y) =y

If x is a real number and (–π/2)< y < π/2, then

tan(-tan x) =x and –tan(tan y) = y

Remember that these properties do not apply for values outside of the intervals given. For instance:

-sin[sin (3 π/2)] = -sin(-1) = - π/2 not 3 π/2

You can also use these properties to re-write a trig function without using trig values. For instance,

sin(-cosx)

-cos x= Θ

x = cos Θ

Adj. = x

Hyp. = 1

= Opp.

= Sine

Graphs of Csc, Sec, Cot and Tan

a = Vertical stretch or compress

b = Horizontal stretch or compress

c = Shifts left or right

d = Shift up or down

CSC Graph

y = csc(x)

SEC Graph

y= sec(x)

TAN Graph

y= tan(x)

COT Graph

y= cot(x)

4.5 Graphs of Sine and Cosine Functions

or

The constant factor of a in y=asinx acts as a scaling factor- a vertical stretch or vertical shrink of the basic sine curve. If , the basic sine curve is stretched, and if , the basic sine curve is shrunk. The result is that the graph of y=asinx ranges between -a and a instead of -1 and 1.

The amplitude of and represents half the distance between the maximum and minimum values of the function and is given by:

Let b be a positive real number. The period of and is given by:

Note that if , the period of is greater than and represents a horizontal stretching of the graph of . Similarly, if , the period of is less than and represents a horizontal shrinking of the graph of .

The constant c creates horizontal translations (shifts) of the basic sine and cosine curves.

The graph of is shifted by an amount of . The number is the phase shift.

The left and right endpoints of a one-cycle interval can be determined by solving the equations and .